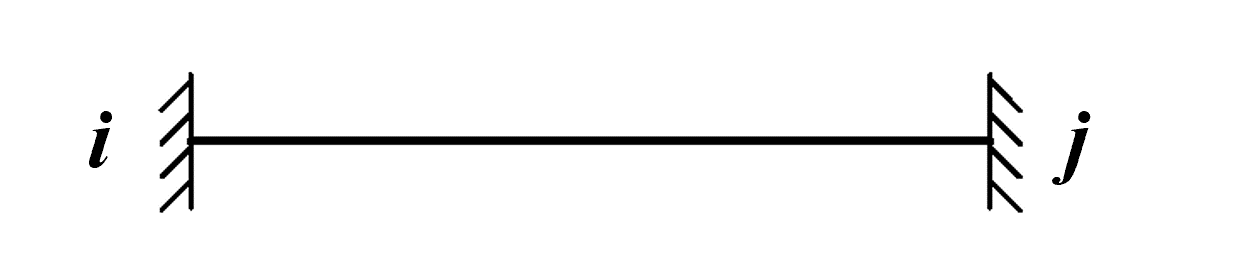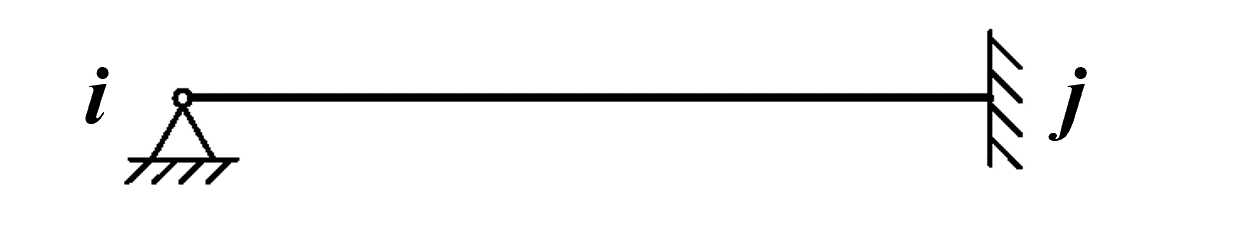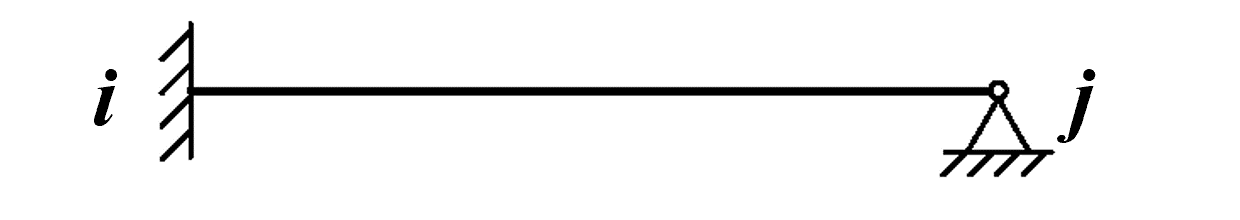1. SDOF振动分析

对单自由度体系进行振动分析，可计算其无阻尼/有阻尼振动响应，以及其在多种类型外力作用下的振动响应。可导出数据或图象信息。

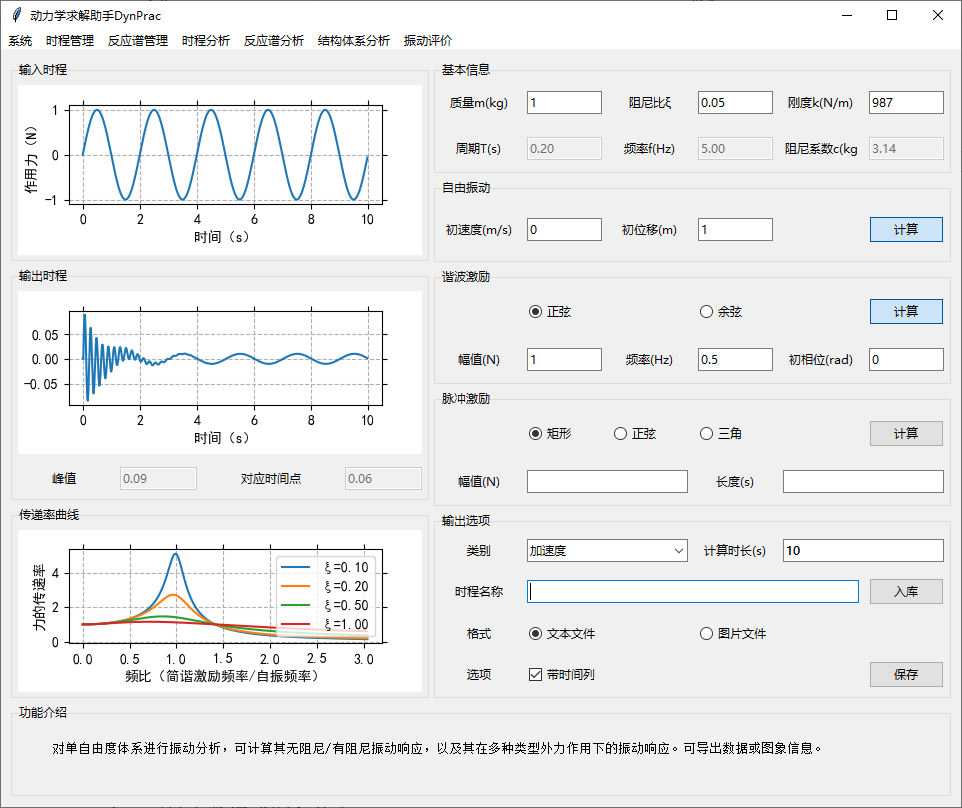
加速度/速度/位移时程计算结果通过“入库”功能追加到现有时程库中。

2. SDOF基底激励

对单自由度体系进行振动分析，可计算其在多种类型基底激励作用下的振动响应，以及其在时程库中的加速度时程作为地面运动加速度输入作用下的振动响应。可导出数据或图象信息。

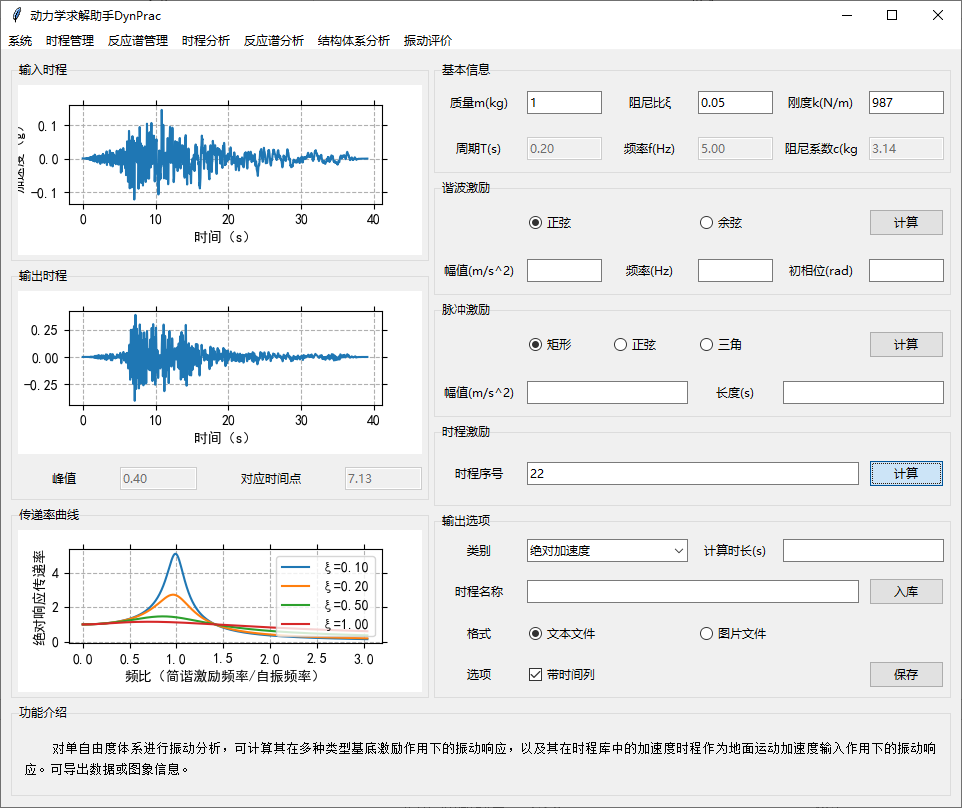
特别地，当采用时程激励输入时，要求必须为加速度时程。此时若不指定计算时长（留空），则默认取为与输入时程长度相同。

加速度/速度/位移时程计算结果通过“入库”功能追加到现有时程库中。

3. MDOF结构建模

3.1.节点信息

以矩阵位移法作为基本原理，实现多自由度结构体系的简化结构建模与计算。节点信息包含坐标位置、质量以及约束的赋予。

节点号要求连续输入，允许存在未利用的节点。

每个节点处可以赋予的属性包括位置坐标、三个方向的质量以及约束情况。

选中“节点列表”中已录入的节点，即可在上方“节点信息”栏目修改其信息，单击“录入”以修改节点信息，或者单击“删除”以删除节点。注意：删除节点会导致后续节点序号前移。

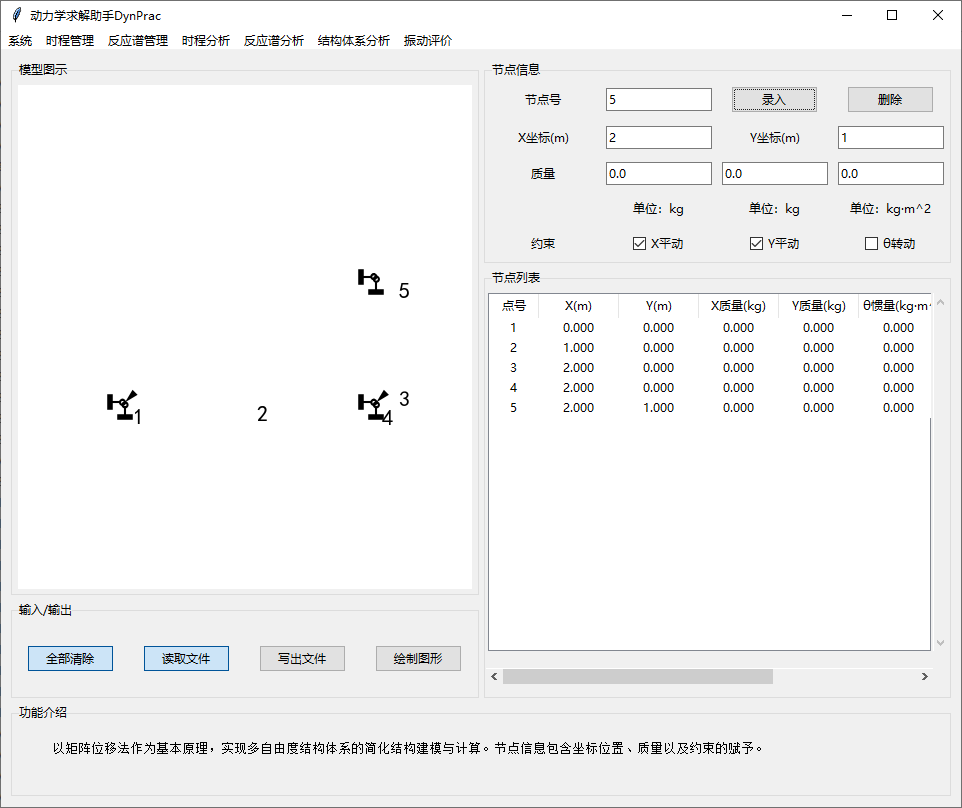
 “输入/输出”操作中，“写出文件”可以将当前已建立好的模型（结构信息与荷载信息）写出到文本文件中保存，“读取文件”可以读取上述已保存的模型文件进行修改或计算。

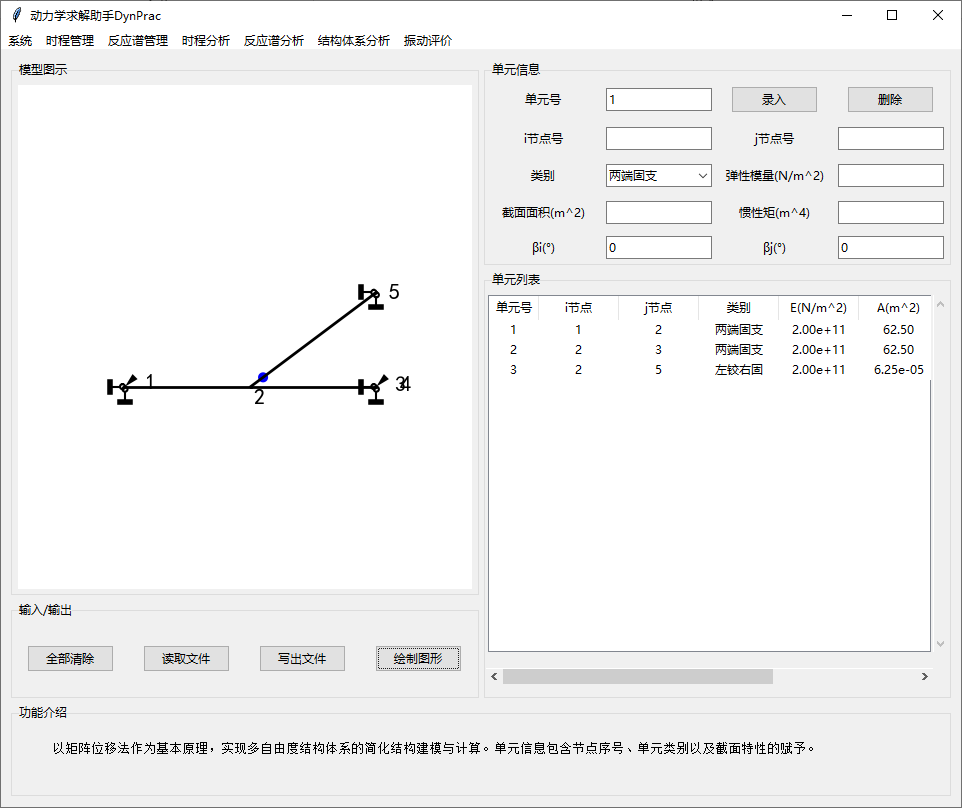
3.2.单元信息

以矩阵位移法作为基本原理，实现多自由度结构体系的简化结构建模与计算。单元信息包含节点序号、单元类别以及截面特性的赋予。

软件中可以选择的杆件单元类型包括以下9类：

节点符号说明见上表。当所选取杆件类型不需要设置β_i或者β_j角度时，该参数自动忽略。

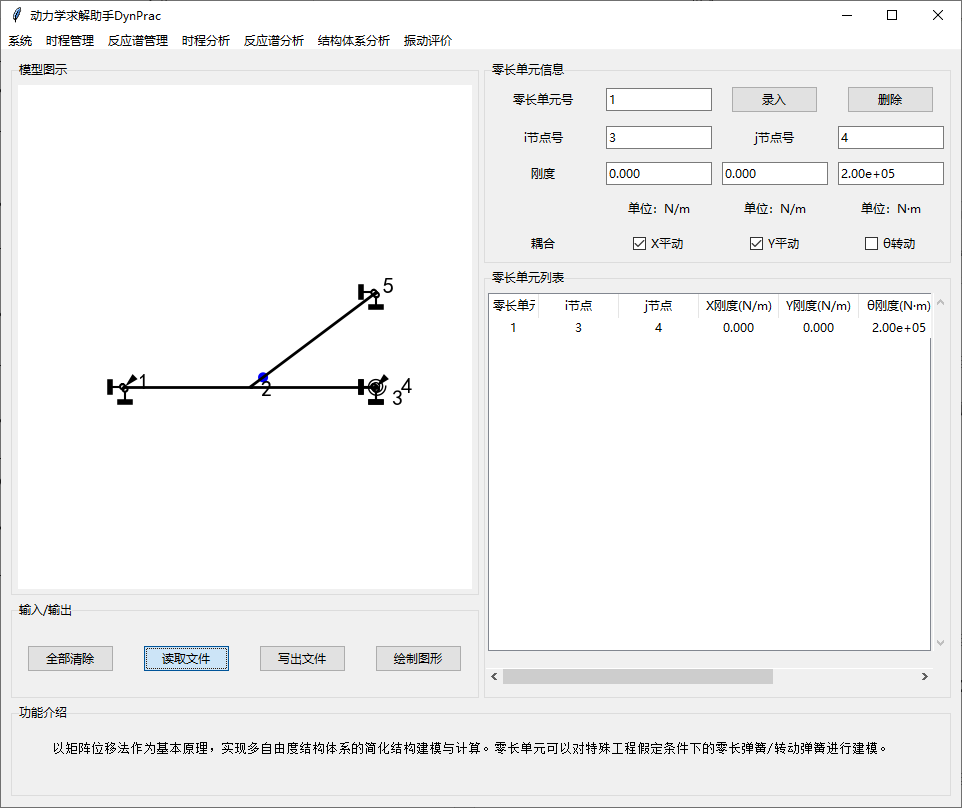
3.3.零长单元

以矩阵位移法作为基本原理，实现多自由度结构体系的简化结构建模与计算。零长单元可以对特殊工程假定条件下的零长弹簧/转动弹簧进行建模。

软件中零长弹簧/转动弹簧的建模均需要指定两个重合的节点，分别与两个杆端、或者将杆端与支座相连接。在需要设置弹簧的自由度上设定刚度，其余方向应指定自由度耦合；若不指定自由度耦合则默认重合节点在该自由度上没有进行连接。

特别需要注意的是，在采用非“两端固支”类别的杆件单元且同时使用了零长单元的情况下，不正确的属性参数设置可能会导致结构体系自由度约束不足，若引起相关计算错误使用者可优先从这一角度着手检查。

4. MDOF荷载布置

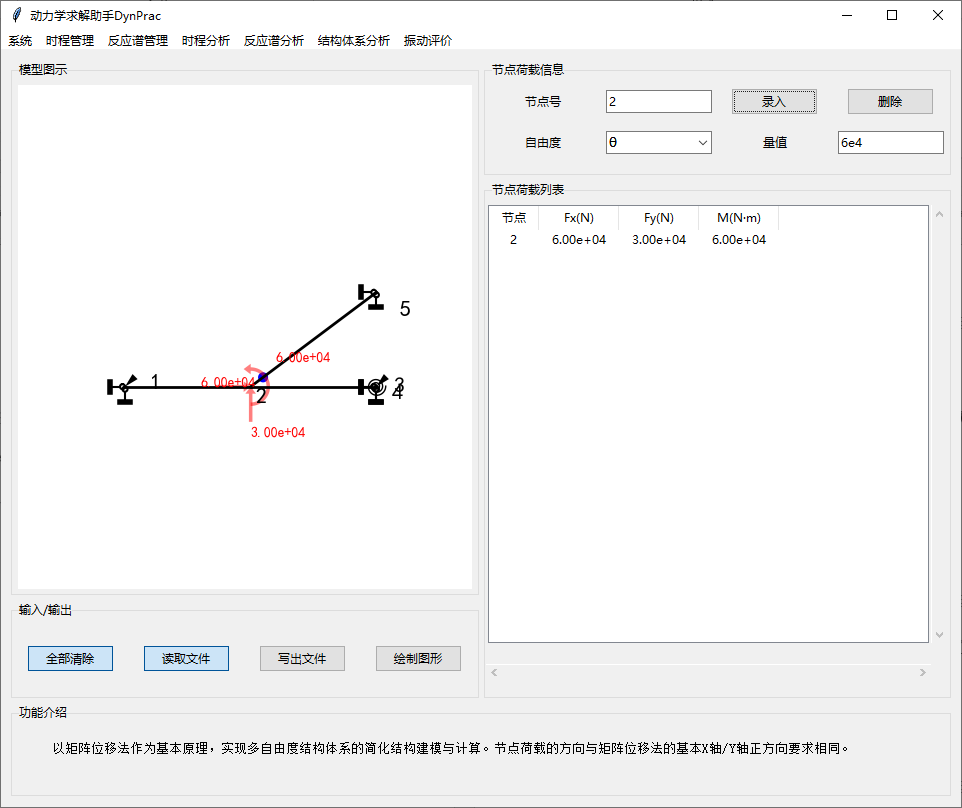
4.1.节点荷载

以矩阵位移法作为基本原理，实现多自由度结构体系的简化结构建模与计算。节点荷载的方向与矩阵位移法的基本X轴/Y轴正方向要求相同。

节点荷载而言，X方向作用力以向右为正方向，Y方向作用力以向上为正方向，弯矩以逆时针旋转为正方向。

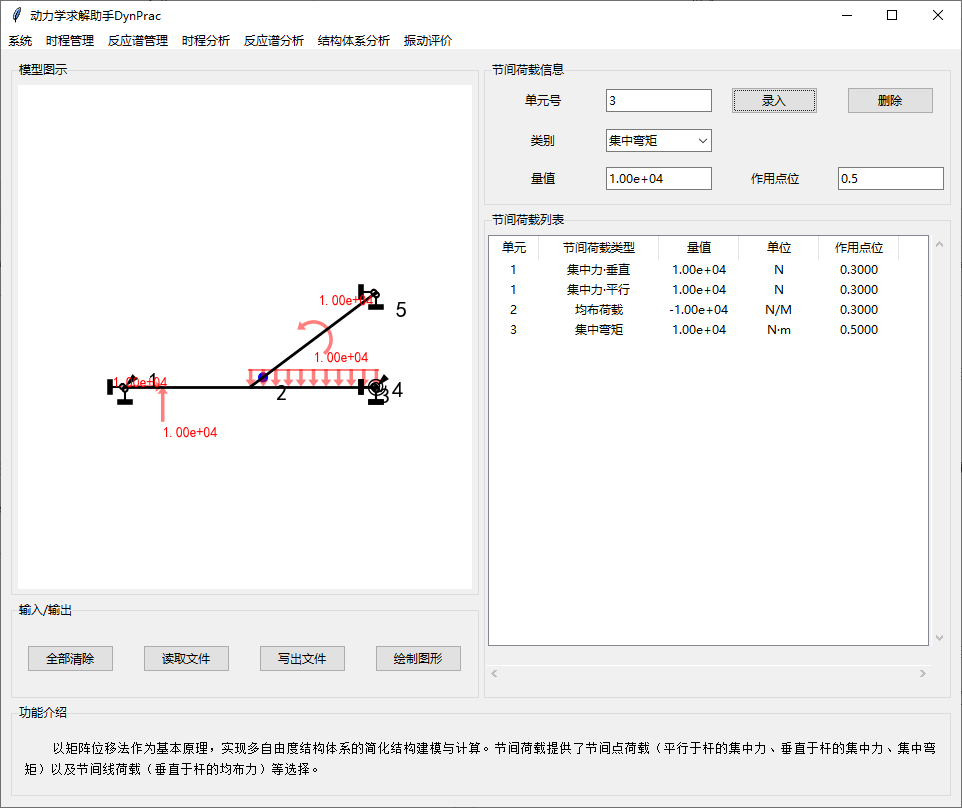
4.2.节间荷载

以矩阵位移法作为基本原理，实现多自由度结构体系的简化结构建模与计算。节间荷载提供了节间点荷载（平行于杆的集中力、垂直于杆的集中力、集中弯矩）以及节间线荷载（垂直于杆的均布力）等选择。

 “集中力·平行”的正方向是所定义杆件单元从i节点指向j节点的方向。

 “集中力·垂直”的正方向是所定义杆件单元从i节点指向j节点的方向逆时针旋转90°后的方向。这与工程中重力荷载的方向往往是相反的，请使用者注意符号设置并检查图中的荷载绘制是否合理。

 “集中弯矩”的正方向是逆时针方向。

 “作用点位”取值范围是(0,1)，0表示i节点位置处，1表示j节点位置处，但不可取0或1，此时应指定为节点荷载而非节间荷载。

 “均布荷载”的正方向与“集中力·垂直”相同，此时“作用点位”参数被忽略。

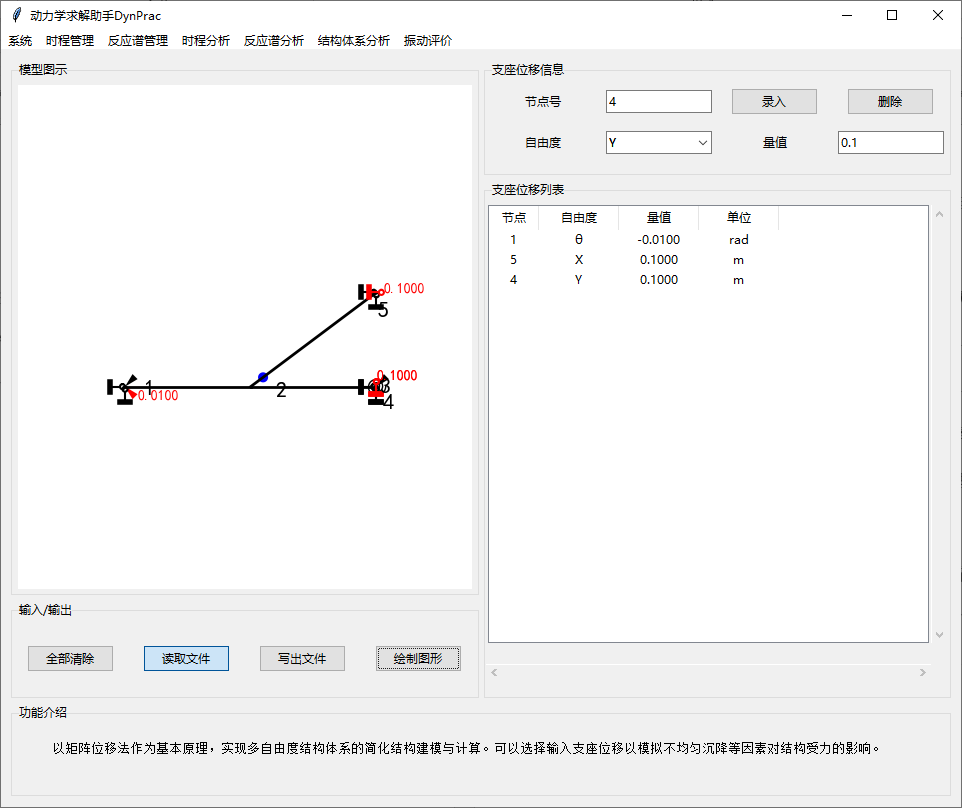
4.3.支座位移

以矩阵位移法作为基本原理，实现多自由度结构体系的简化结构建模与计算。可以选择输入支座位移以模拟不均匀沉降等因素对结构受力的影响。

支座位移的正方向为：X方向支座位移以向右为正，Y方向支座位移以向上为正，支座转角以逆时针旋转为正。

5. MDOF静力分析

以矩阵位移法作为基本原理，实现多自由度结构体系的简化结构建模与计算。静力分析可以对前述模型和荷载条件下的结构体系进行计算分析。

静力计算后可以保存相关图片文件或者以文本文件格式保存表格中的计算结果数据。

节点位移计算结果的方向与整体坐标系方向一致，X方向位移以向右为正，Y方向位移以向上为正，转角以逆时针旋转为正。

单元内力计算结果，轴力以使杆件受拉为正，剪力以使杆件脱离体截面顺时针旋转为正，弯矩取其绝对值大小，并参考弯矩图判断其方向，弯矩图曲线绘制于杆件受拉一侧。

由于采用了数值计算方法，可能出现数量级很小的舍入误差，例如桁架杆端出现1×10^-11数量级的弯矩等，此时使用者应依结构力学概念舍去取为0值。

特别地，“变形图”中不仅包括杆件受弯产生的挠度，也包括杆件端节点位移引起的刚体变形，从而反应结构整体变形的结果。

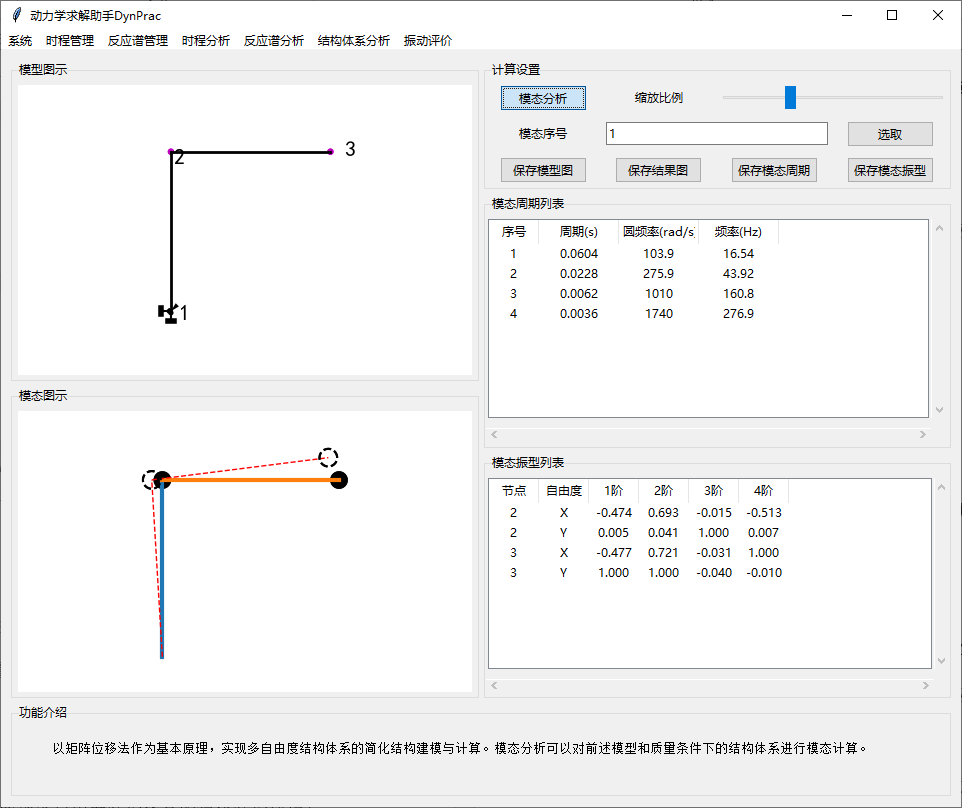
6. MDOF模态分析

以矩阵位移法作为基本原理，实现多自由度结构体系的简化结构建模与计算。模态分析可以对前述模型和质量条件下的结构体系进行模态计算。

切换模型序号以绘制各个模态的示意图。

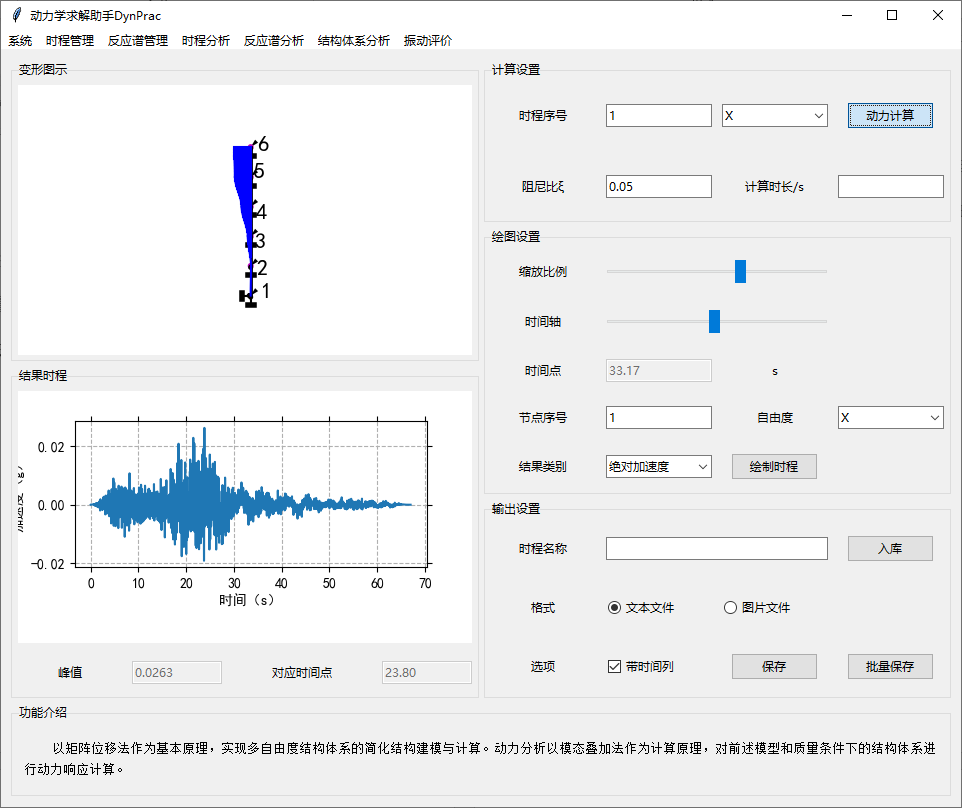
7. MDOF动力分析

以矩阵位移法作为基本原理，实现多自由度结构体系的简化结构建模与计算。动力分析以模态叠加法作为计算原理，对前述模型和质量条件下的结构体系进行动力响应计算。

动力分析计算需要从时程库中选定时程并指定阻尼比。移动时间轴滑块可以绘制结构在不同时刻的变形图示。

选取节点、自由度以及结果类别后的计算结果绘制于左下图中，并可进一步储存到时程库中或输出为图片/文本文件。